Invertible Image Signal Processing
CVPR 2021

The Hong Kong University of Science and Technology

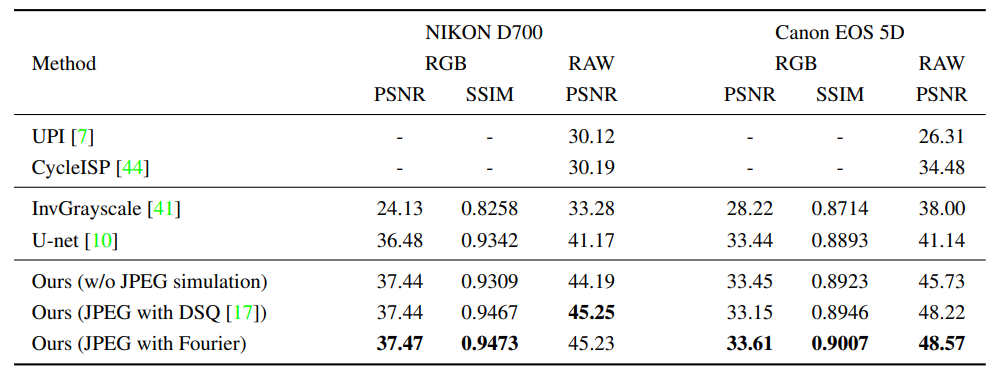
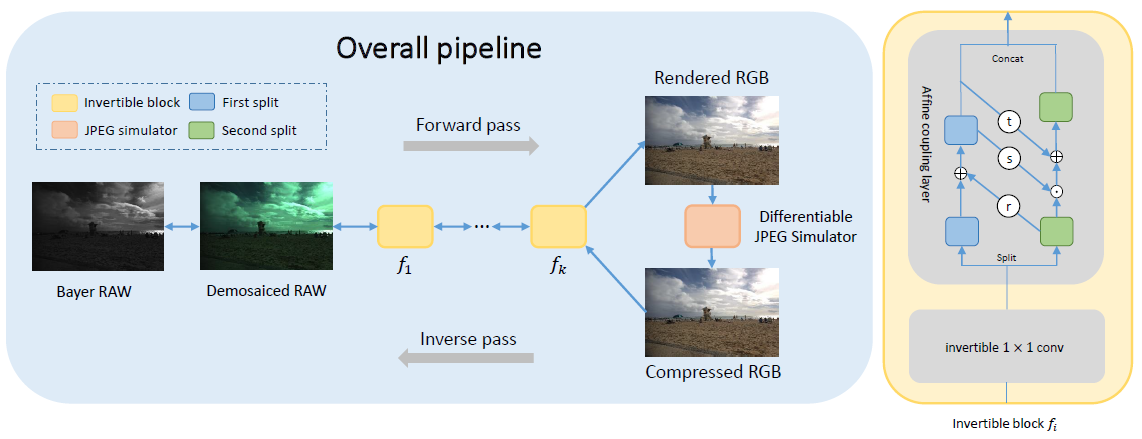
overview

Abstract

Unprocessed RAW data is a highly valuable image format for image editing and computer vision. However, since the file size of RAW data is huge, most users can only get access to processed and compressed sRGB images. To bridge this gap, we design an Invertible Image Signal Processing (InvISP) pipeline, which not only enables rendering visually appealing sRGB images but also allows recovering nearly perfect RAW data. Due to our framework's inherent reversibility, we can reconstruct realistic RAW data instead of synthesizing RAW data from sRGB images, without any memory overhead. We also integrate a differentiable JPEG compression simulator that empowers our framework to reconstruct RAW data from JPEG images. Extensive quantitative and qualitative experiments on two DSLR demonstrate that our method obtains much higher quality in both rendered sRGB images and reconstructed RAW data than alternative methods.

Results

overview

The qualitative comparison among UPI, CycleISP and our method. UPI and CyleISP synthesize RAW data from 8-bit compressed RGB, which is inevitable to suffer from the information loss of traditional ISP. Unlike theirs, our model forms a RAWRGB-RAW cycle and is inherently reversible to recover the realistic RAW image. The GT RAW image is visualized through bilinear demosaicing, and other RAW images are visualized through error maps.
overview

Quantitative evaluation among our model and baselines. Various perceptual metrics show that our proposed ISP model outperforms all the baselines. Our method with JPEG simulation using proposed Fourier quantization outperforms the other two alternative models.

Extended results on low-light enviornments

overview

Our approach also performs well under low-light environments.

Extended results on video ISPs

overview

We extend our invertible ISP to videos where our proposed video normalizing flow method can achieve desirable balance among RGB video rendering, RAW video reconstruction, and temporal consistency. Our invertible framework is robust to the information lost due to video compression in digital cameras. To our best knowledge, we propose the first framework for accurate RAW video reconstruction from compressed video files.

Method

overview

Our Invertible ISP (InvISP) framework. InvISP is composed of both forward and inverse passes. In the forward pass, the Bayer RAW is first bilinearly demosaiced and then transformed to an RGB image by a stack of bijective functions $\{f_i\}^k_{i=0}$. Our model integrates a differentiable JPEG simulator to account for compression information lost. During the training time, to invert the ISP, the backward pass takes a compressed RGB image as input and reverses all the bijective functions and the bilinear demosaicing to obtain the original RAW image. Note that the backward pass takes real JPEG images as input at test time. We illustrate the details of the invertible block on the right. $r$, $s$, and $t$ are transformations defined in the bijective functions $\{f_i\}^k_{i=0}$.
The website template was borrowed from Michaël Gharbi.